Curso- RStudio

May 23, 2023

Este lenguaje es conocido por su amplia gama de paquetes estadísticos. Es un lenguaje especialmente adecuado para el análisis estadístico y la implementación de algoritmos complejos. Si estás interesado en el análisis exploratorio de datos, pruebas de hipótesis, modelado predictivo o cualquier otro aspecto estadístico, R te brinda las herramientas necesarias para llevar a cabo estos análisis de manera eficiente ademas R cuenta con una comunidad activa y comprometida de usuarios en todo el mundo. Esto significa que hay una gran cantidad de recursos disponibles, como paquetes, tutoriales, foros de discusión y blogs, que pueden ayudarte a resolver problemas y aprender de forma autodidacta.

Indice

R como calculadora
Funciones basicas
Estructura de datos
- Vectores
  - Operadores Logicos

Creando variables y utilizando `R` como calculadora

A <- 9 # Asignamos el valor a nuestra variable A
B <- 10 # Asignamos el valor a nuestra variable B

Suma = A + B # Realizamos la operación deceada y guardamos el valor 
Suma # Mostramos el resultado en la consola

Podemos seguir haciendo operaciones con nuestros valores guardados A y B

Resta  = A - B 
Multiplicacion = A * B
Division = A / B
Potencia = A ^ B

Funciones basicas

sqrt(A) #Raíz cuadrada de A
log(A) #Logaritmo narural de A
log10(A) #Logaritmo base 10 de A
abs(A) #Valor absoluto de A
factorial(A) # Factorial de A

Creando funciones

Podemos crear nuestras propias funciones para adaptarlas a lo que necesitemos. Vamos a crear una función que resuelva ecuacion de segundo grado, tomando como referencia la fórmula general para resolver la ecuación.

X_1 = function(a,b,c){(-b-sqrt(b^2-4*a*c))/(2*a)}
X_2 = function(a,b,c){(-b+sqrt(b^2-4*a*c))/(2*a)}
C <- 2 #La variables "A" y "B" siguen cargadas en nuestro "Environment"

Mandamos llamar a nuestra función de la siguiente forma:

X_1(A,B,C)
[1] -0.8495279
X_2(A,B,C)
[1] -0.2615832

También podemos acceder a nuestras funciones sin asignar los coeficientes a una variable, por ejemplo:

X_1(1,3,1)
[1] -2.618034
X_2(1,3,1)
[1] -0.381966

Podemos ingresar condiciones a nuestra función, por ejemplo; en caso de que nuestro discriminante sea positivo ejecutar el programa y mostrar los resultados junto con su gráfica, en caso contrario, mostrar un mensaje indicando que las soluciones son imaginarias.

ecuacion_segundo_grado <- function(a, b, c) { #damos los mismos paramentros de entrada
  discriminante <- b ^ 2 - 4 * a * c #calculamos el discriminante y lo guardamos en una variable
  
  if (discriminante >= 0) { #si el discriminante es positivo calculara las soluciones
    solucion_1 <- (-b + sqrt(discriminante)) / (2 * a)
    solucion_2 <- (-b - sqrt(discriminante)) / (2 * a)
    
    cat("Las soluciones de la ecuación son:", solucion_1, "y", solucion_2, "\n") #imprime las soluciones
    
    #Las graficas las vamos a abarcar más a fondo en ejemplos posteriores solo es un ejemplo de lo que se le pueden integrar a las funciones
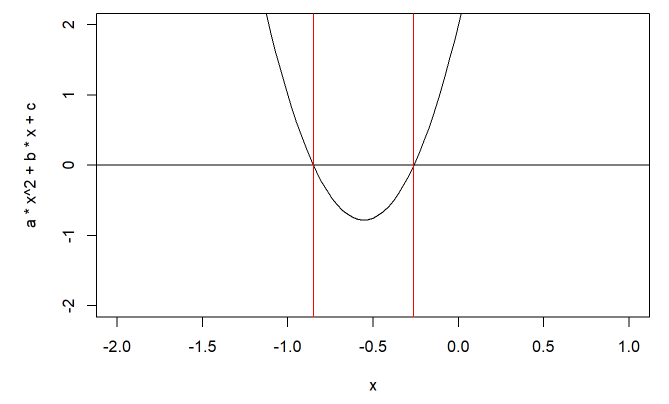
    # Grafica la función
    curve(a*x^2 + b*x + c, xlim = c(-2, 1), ylim = c(-2, 2))
    
    # Muestra las intersecciones con el eje x
    abline(h = 0)
    abline(v = solucion_1, col = "red") 
    abline(v = solucion_2, col = "red")
  } else { #caso contrario (discriminante negativo)
    cat("La ecuación tiene soluciones imaginarias.\n")
  }
}
#Ejecutamos nuestro ejemplo inicial
ecuacion_segundo_grado(9, 10, 2)

Las soluciones de la ecuación son: -0.2615832 y -0.8495279 

Estructura de datos

Vectores

Un vector es una secuencia ordenada de datos. R dispone de muchos tipos de datos, por ejemplo:

logical : lógicos(TRUE o FALSE)
integer : números enteros
numeric : números reales
complex : números complejos
character : palabras

En Rtodos los objetos del vector han de ser del mismo tipo.

c(6,2,7)
[1] 6 2 7

Los índices de R empiezan en 1 para acceder a los elementos de un vector tenemos lo siguente:

vector[i] : da la i-ésima entrada del vector.
vector[-i] : si i es un número, este subvector está formado por todas las entradas del vector original menos la entrada i-ésima.

Operadores lógicos

== : Igual que
!= : Distinto de
>= : Mayor igual que
<= : Menor igual que
> : Mayor que
< : Menor que
! : NO lógico
& : Y lógico
| : O lógico

Podemos utilizar operadores lógicos que es una forma de “condicionar” a los vectores, así con una seria de instrucciones lógicas podemos acceder solo a los datos que necesitemos de dicho vector.

v = c(1,2,3,4,3,2,4,2,3,3) #Creamos a nuestro vector y lo asignamos a una variable

Queremos que nos muestre solo los valores que sean igual a tres

v [v == 3]
[1] 3 3 3 3

Ahora vamos a decirle a R que sume 10 a las posiciones 2,3,4 del vector

v[2:4] = v[2:4] + 10
v
[1]  1 12 13 14  3  2  4  2  3  3

Agregar un nuevo valor al vector

v[length(v)+1] = 100 #agregar 100 a la ultima posición + 1

Osvaldo Yañez